Graphs And Transformations Flashcards Quizlet
The simplest Quadratic Equation is f (x) = x 2 And its graph is simple too This is the curve f (x) = x2 It is a parabola Now let us see what happens when we introduce the a value f (x) = ax2 Larger values of a squash the curve inwards Smaller values of a expand it outwardsExplanation The equation of a circle is given by (x −h)2 (y −k)2 = r2 with center (h,k) and radius r We have the equation x2 y2 = 100, where the origin is our center since we have no h or k value We also know from √100 that we have radius 10 We can now graph this circle knowing we are centered at the origin, and we have a radius
(x-h)^2+(y-k)^2=r^2 graph
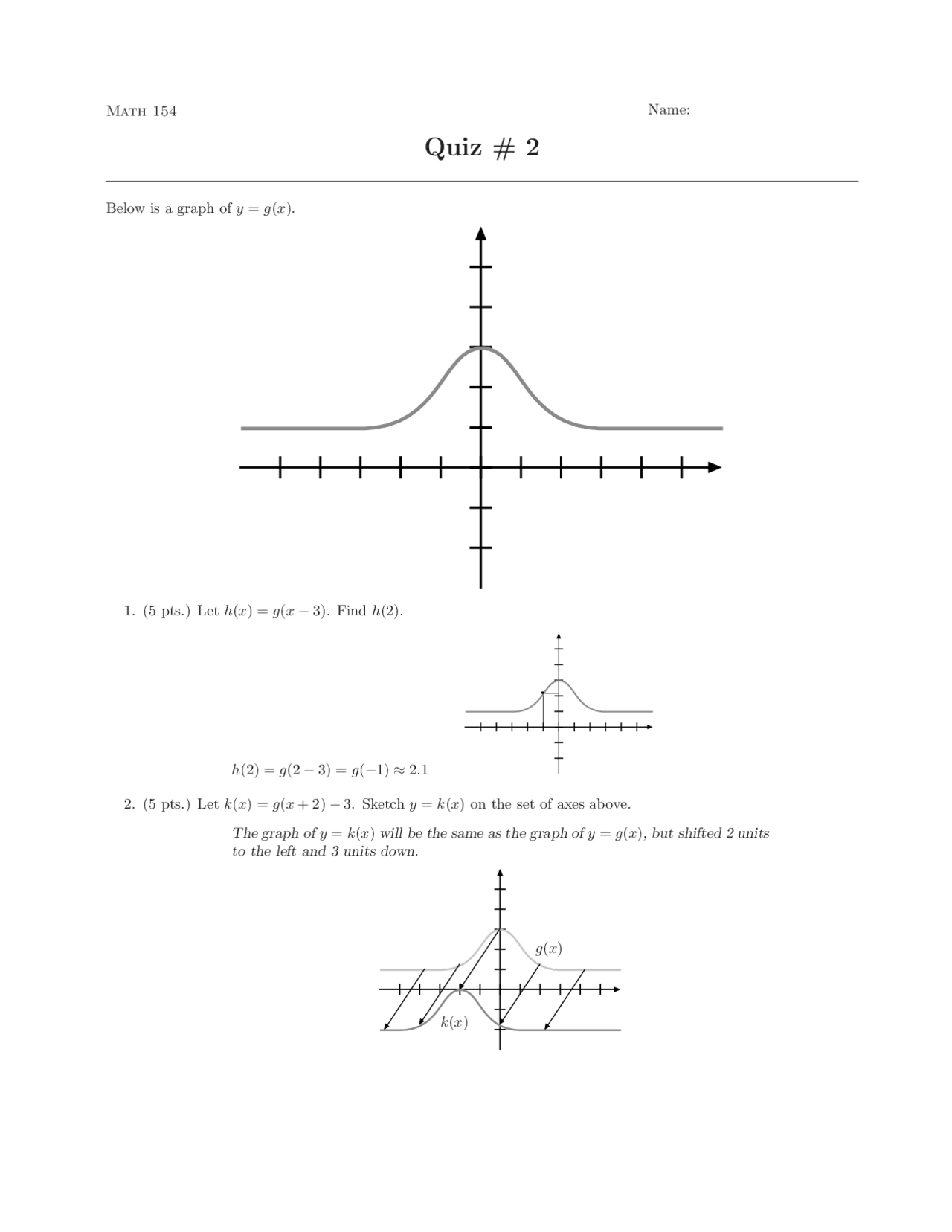
(x-h)^2+(y-k)^2=r^2 graph-Section 21 Transformations of Quadratic Functions 51 Writing a Transformed Quadratic Function Let the graph of g be a translation 3 units right and 2 units up, followed by a refl ection in the yaxis of the graph of f(x) = x2 − 5xWrite a rule for g SOLUTION Step 1 First write a function h that represents the translation of f h(x) = f(x − 3) 2 Subtract 3 from the inputAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ±
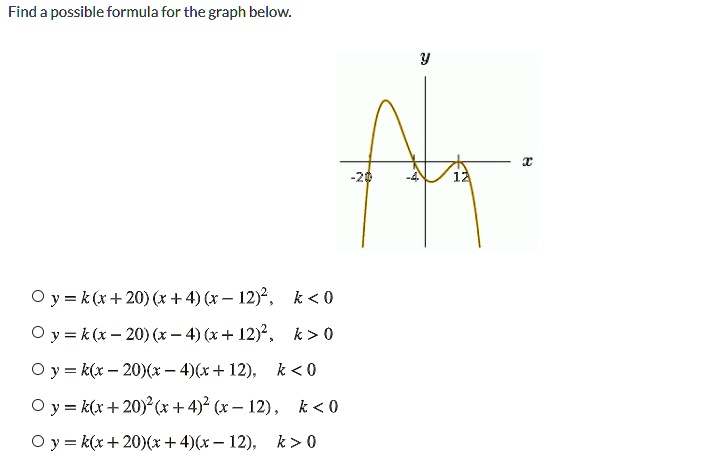
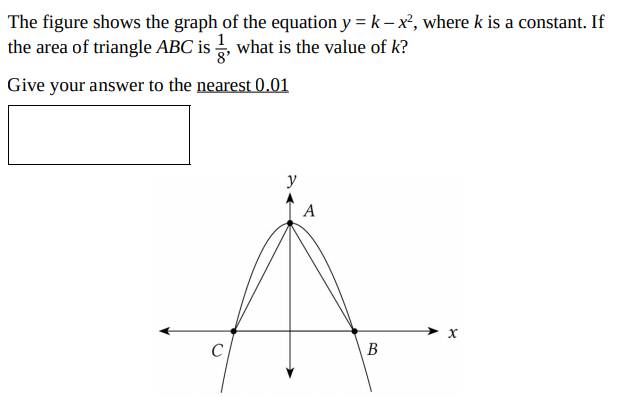
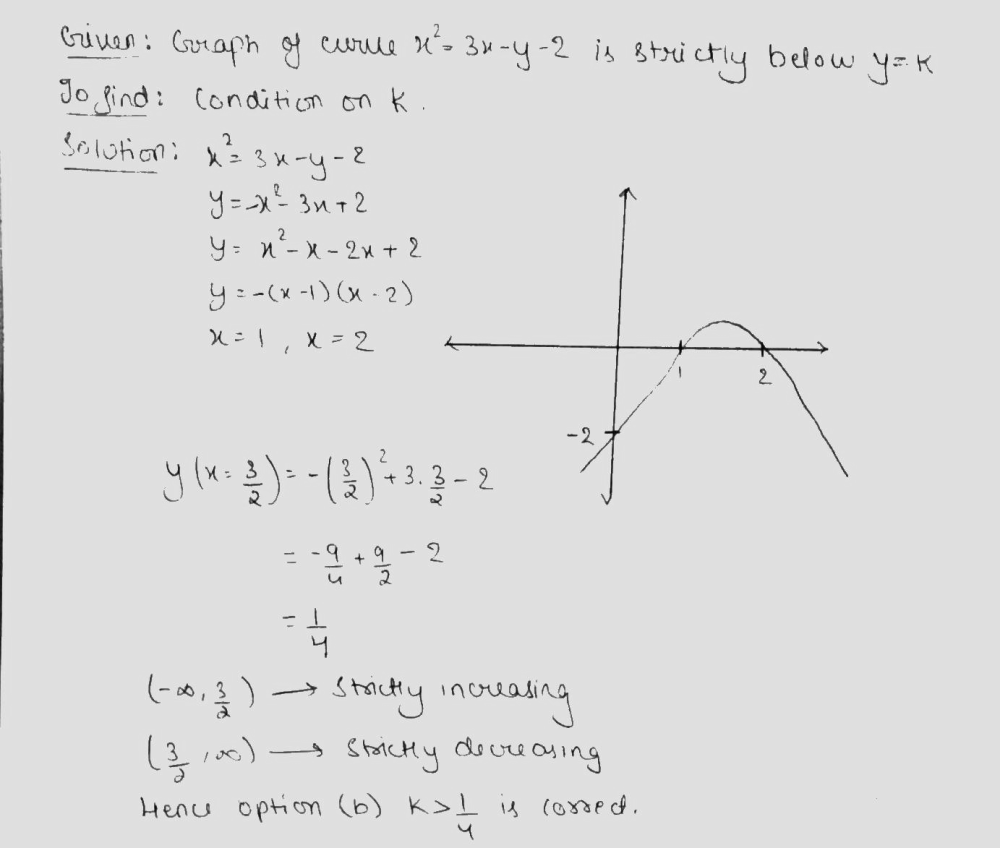
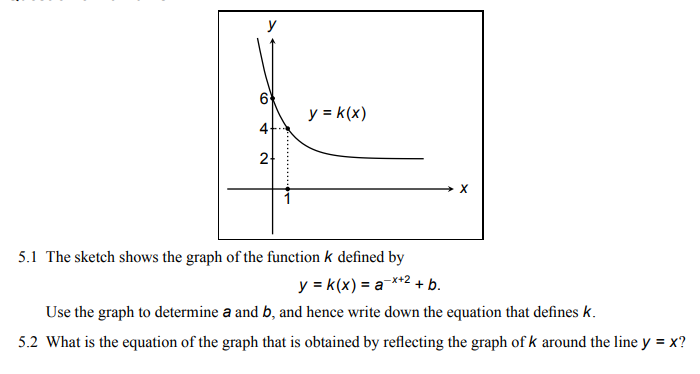
5 1 The Sketch Shows The Graph Of The Function K D Gauthmath
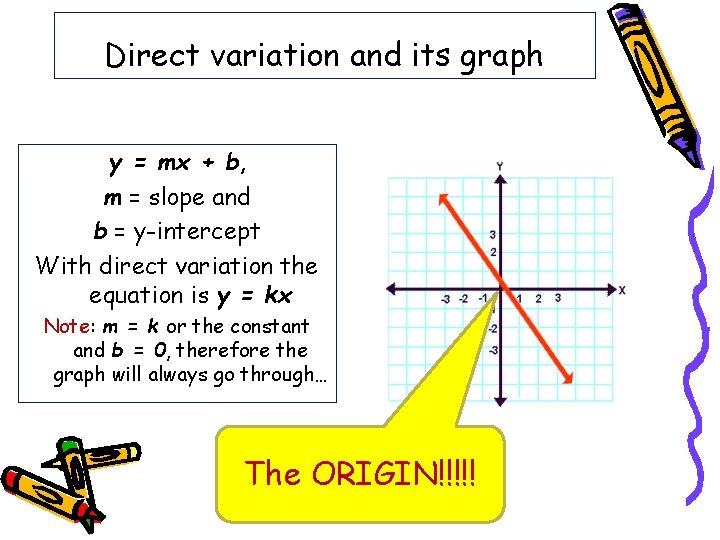
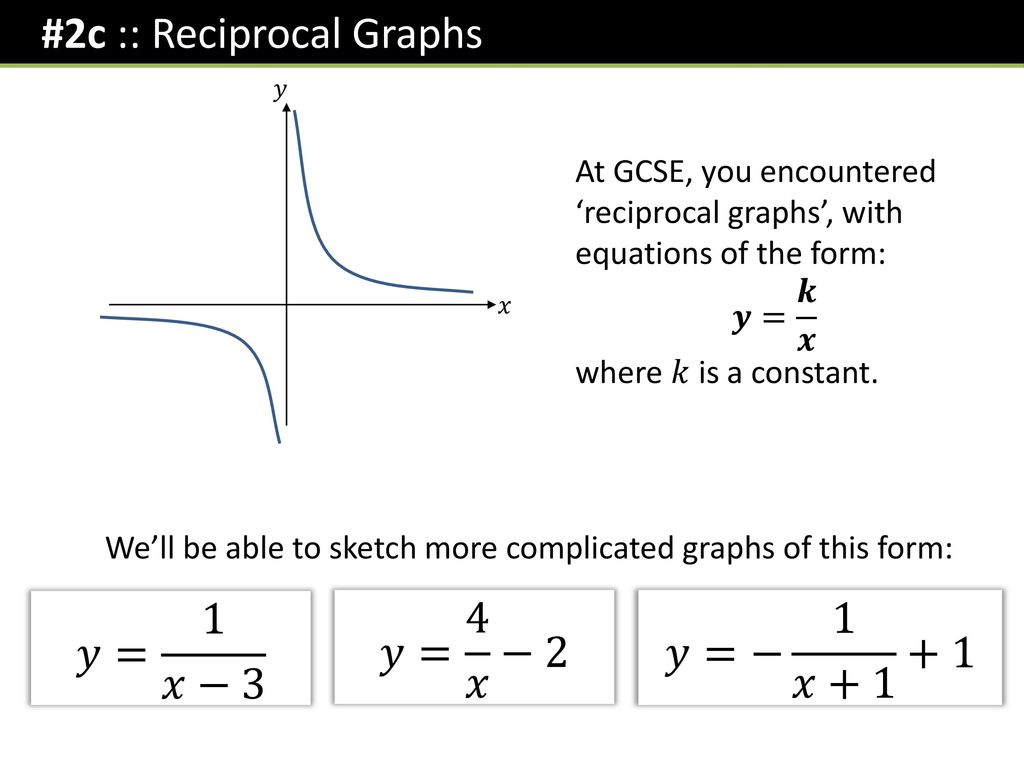
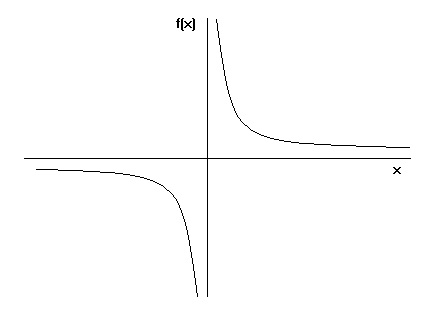
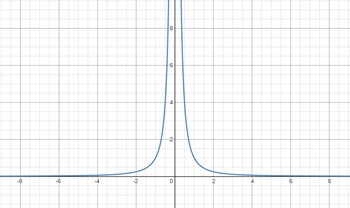
The graph of the equation (xh)^2/ (a^2) (yk)^2/b^2 = 1 is an ellipse with center (h,k), horizontal axis length 2a, and vertical axis length 2b Find parametric equations whose graph is an ellipse with center (h,k), horizontal axis length 2a, and vertical axis length 2b, and explain why your answer is correctExplanation Probably you can recognize it as the equation of a circle with radius r = 1 and center at the origin, (0,0) The general equation of the circle of radius r and center at (h,k) is (x −h)2 (y −k)2 = r2 Answer linkA lesson of the graph y=k/x Blog How to schedule fewer meetings and get more done;
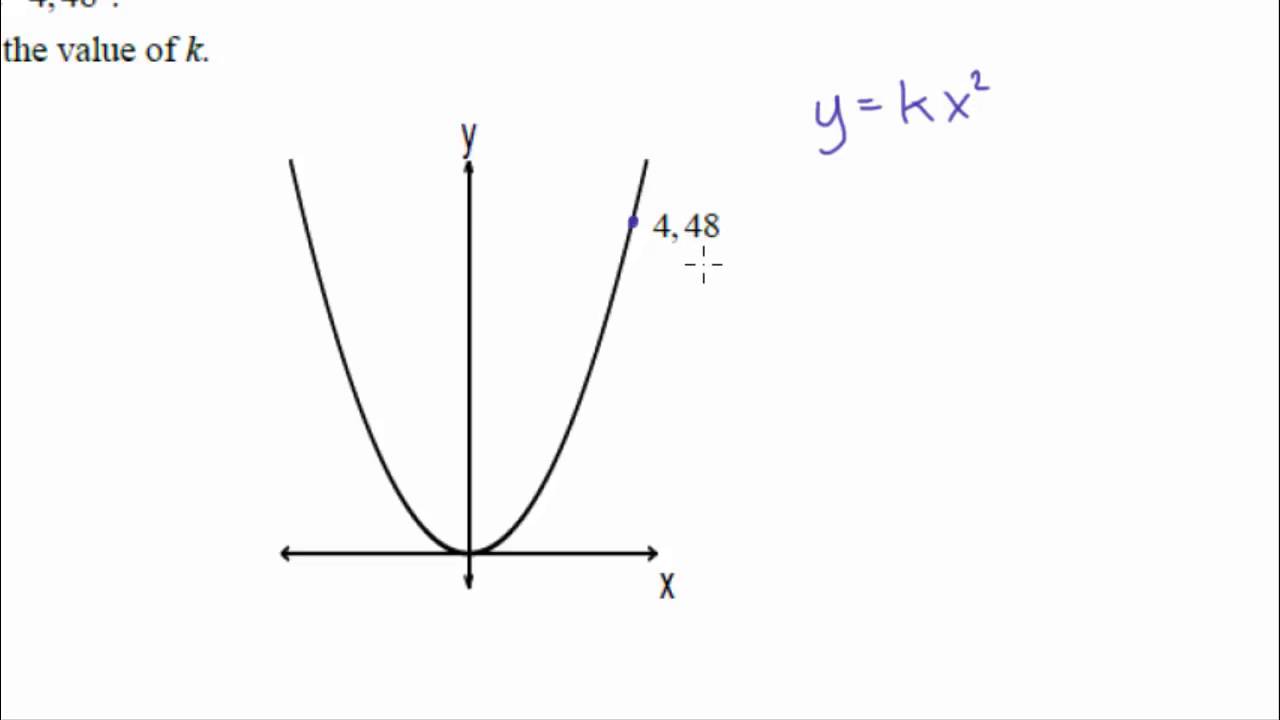
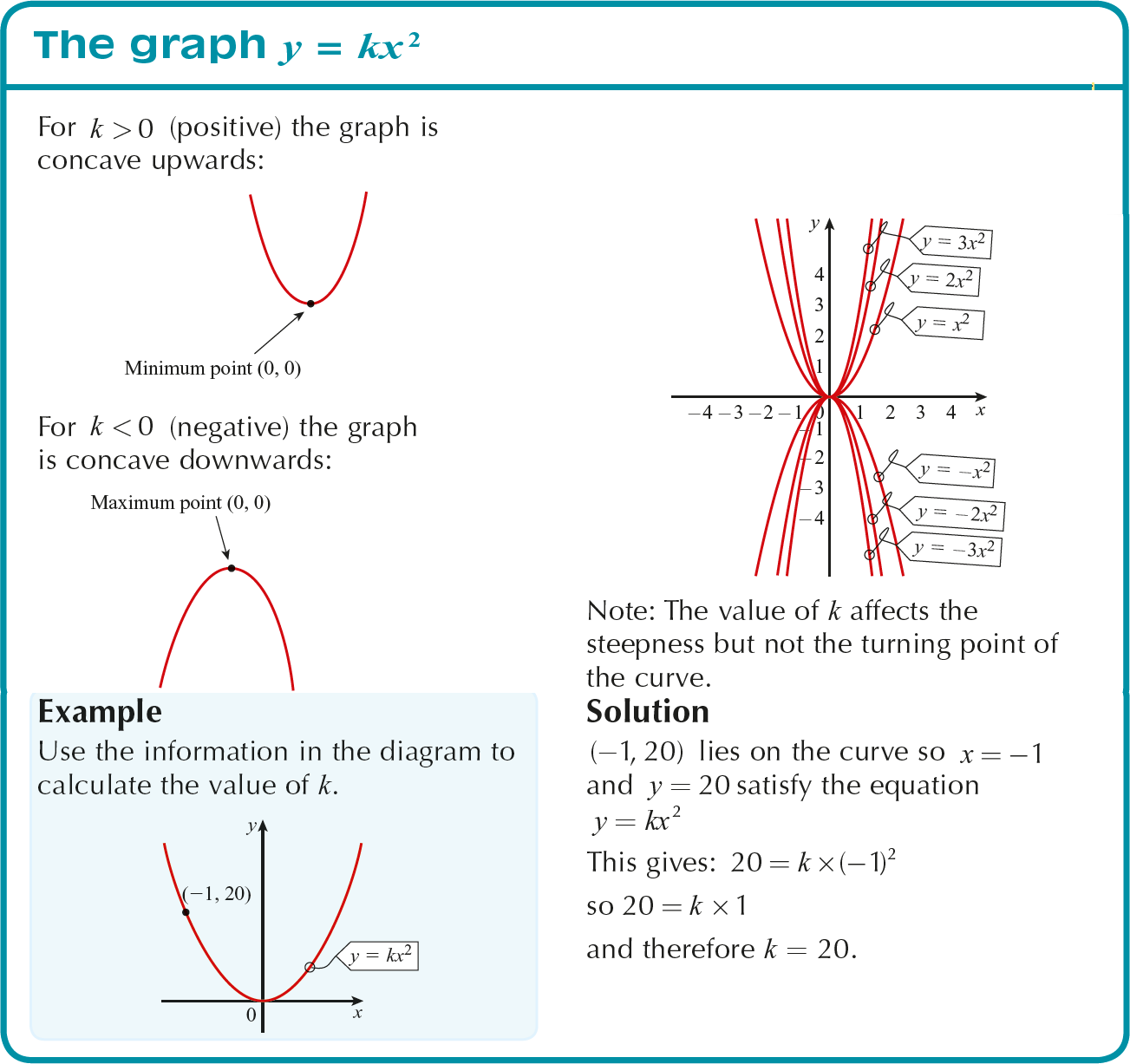
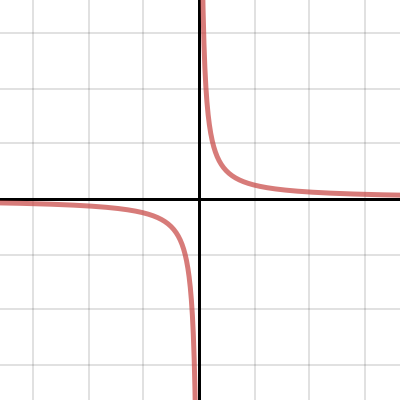
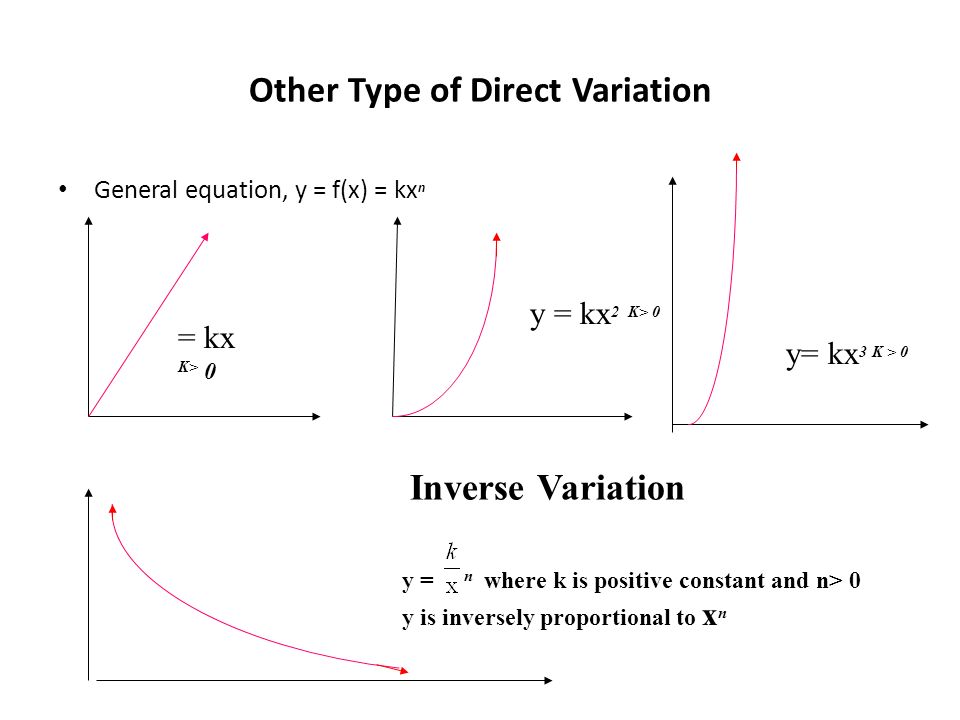
Steps to graph x^2 y^2 = 42_5 The Graph of y=kx^2Analyzing the Graphs of y = sec x and y = cscx The secant was defined by the reciprocal identity sec x = 1 cos x sec x = 1 cos x Notice that the function is undefined when the cosine is 0, leading to vertical asymptotes at π 2, π 2, 3 π 2, 3 π 2, etc Because the cosine is never more than 1 in absolute value, the secant, being the reciprocal, will never be less than 1 in absolute value
(x-h)^2+(y-k)^2=r^2 graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
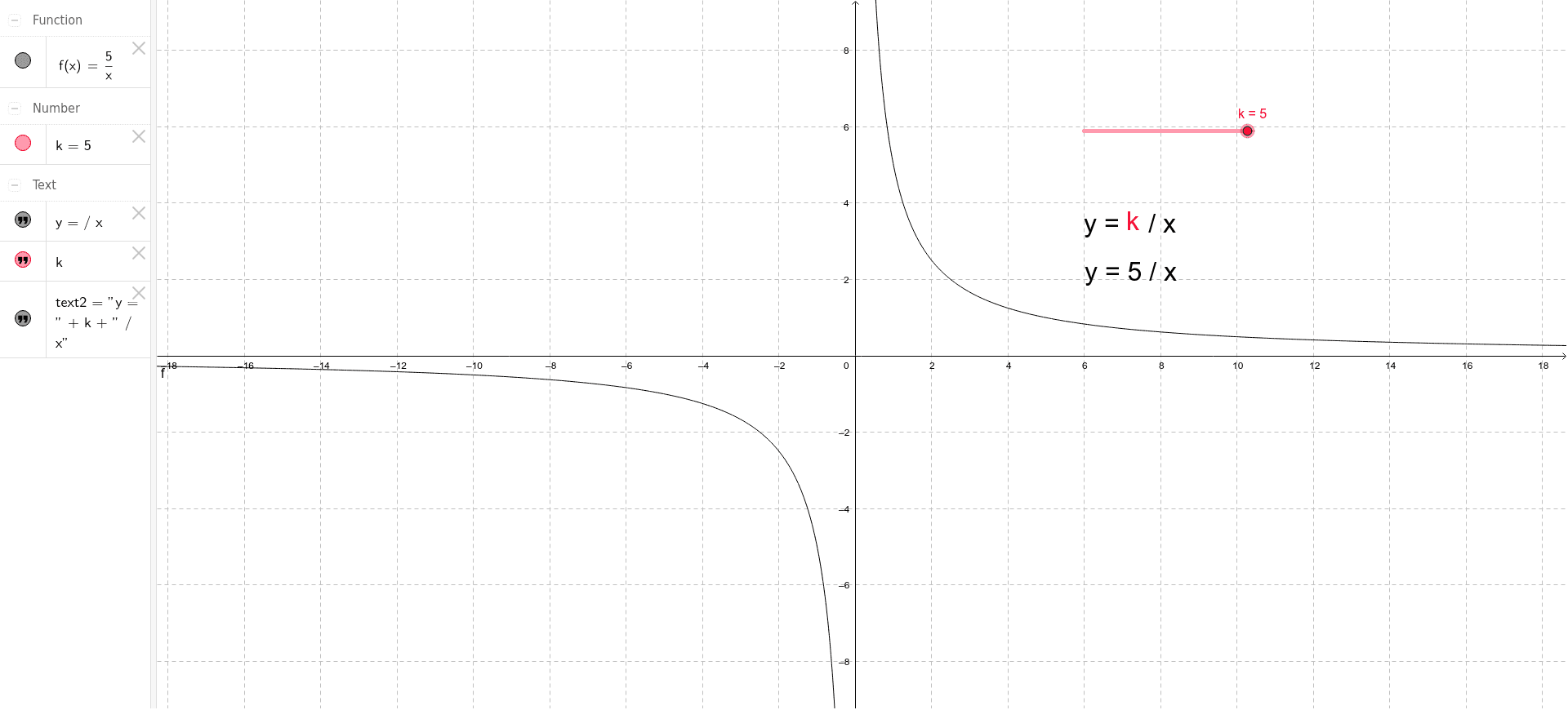「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
.svg "13 02 Relations In The Form Of Y Kx N For N In 2 1 1 2 3 Year 12 Maths Vce Further Mathematics 3 4 Edition Mathspace") |  | |
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
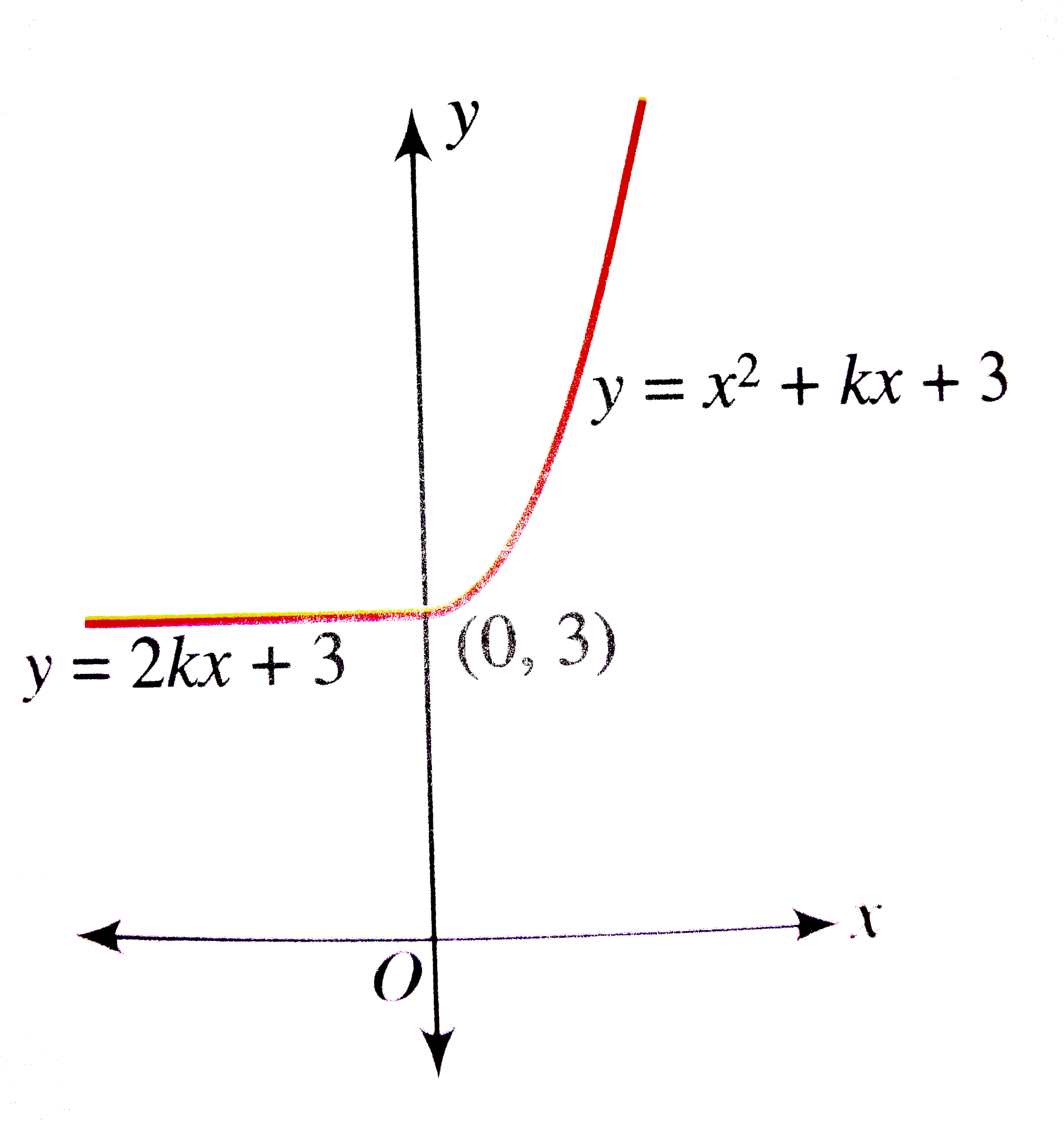.svg 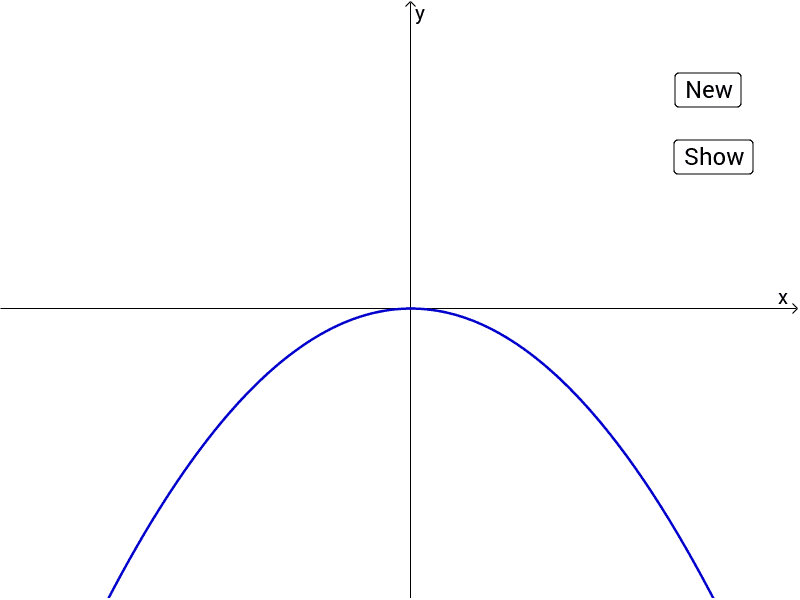"13 02 Relations In The Form Of Y Kx N For N In 2 1 1 2 3 Year 12 Maths Vce Further Mathematics 3 4 Edition Mathspace") |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
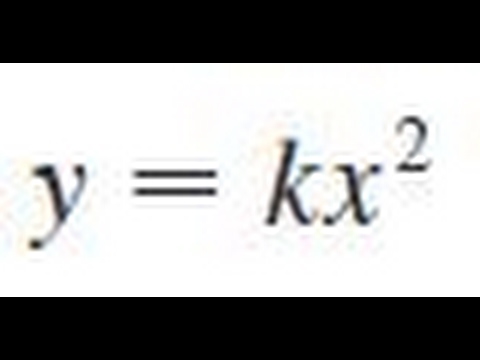「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「(x-h)^2+(y-k)^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
|  |  |
 |
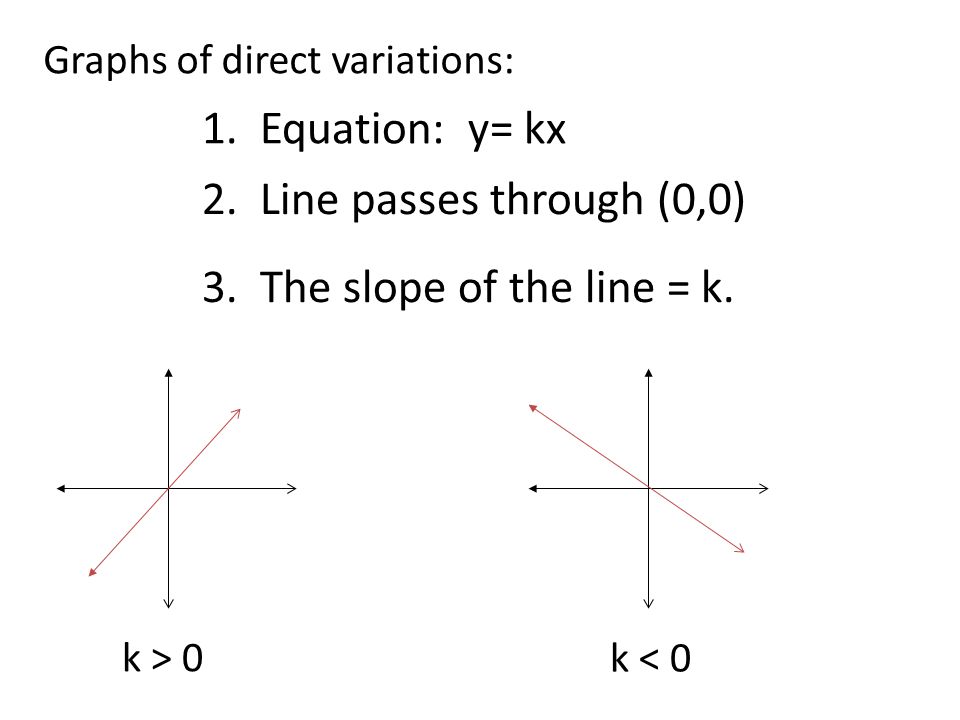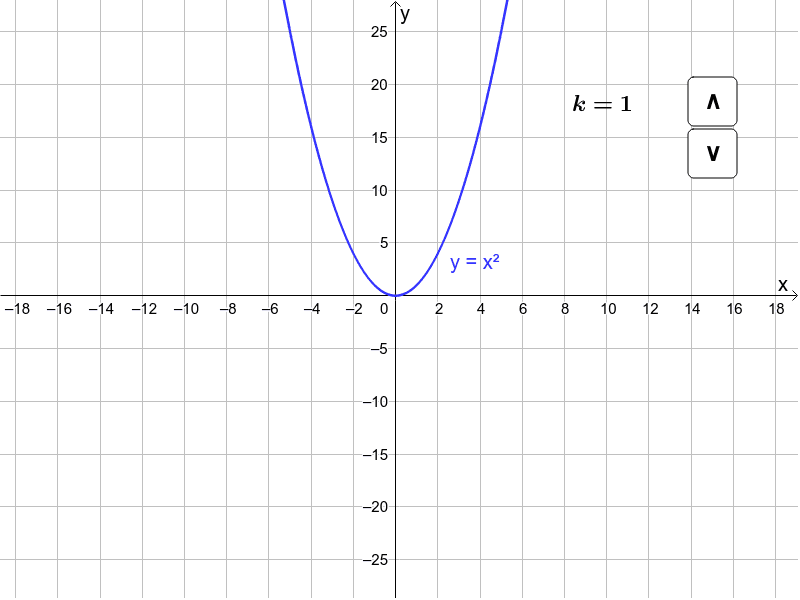
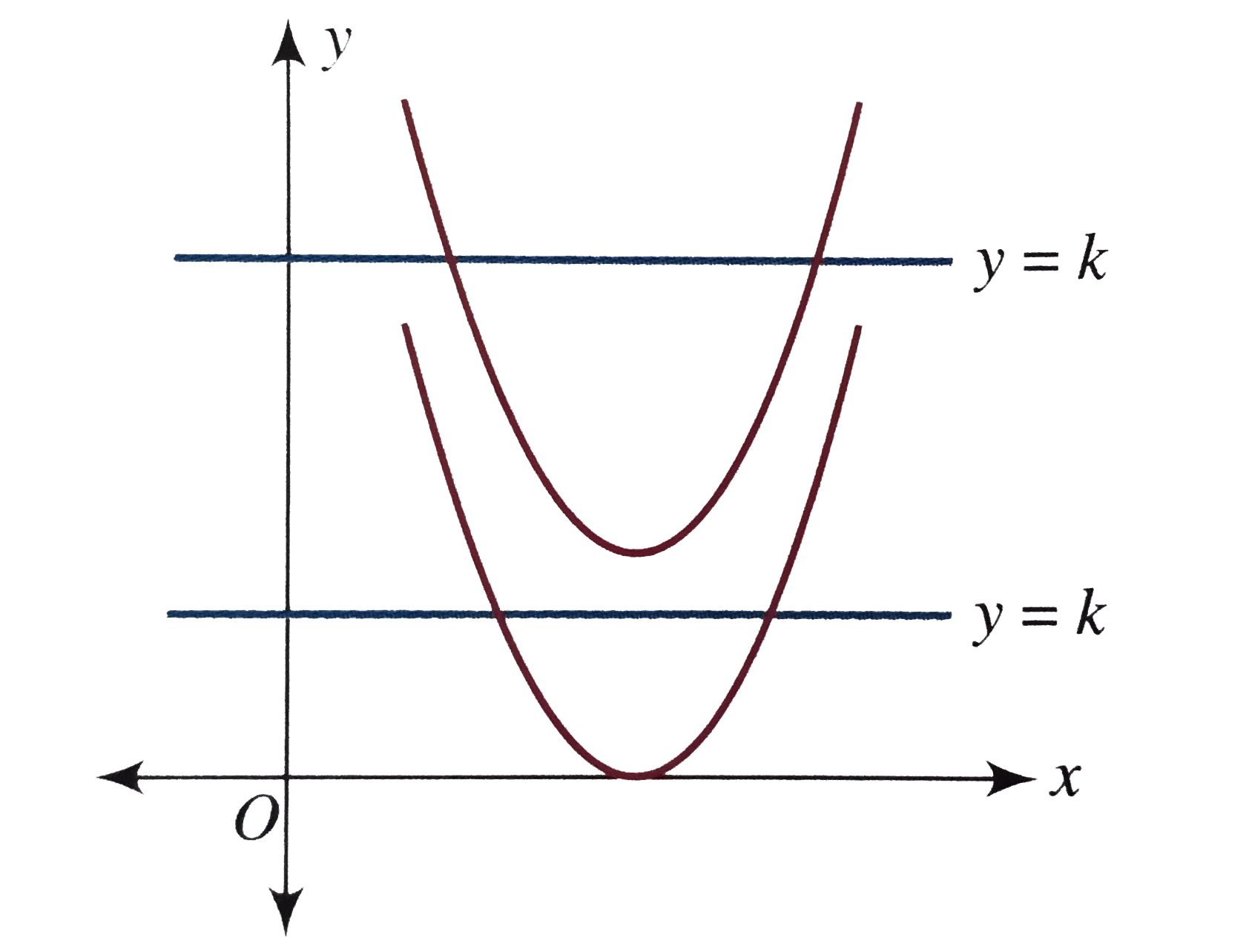
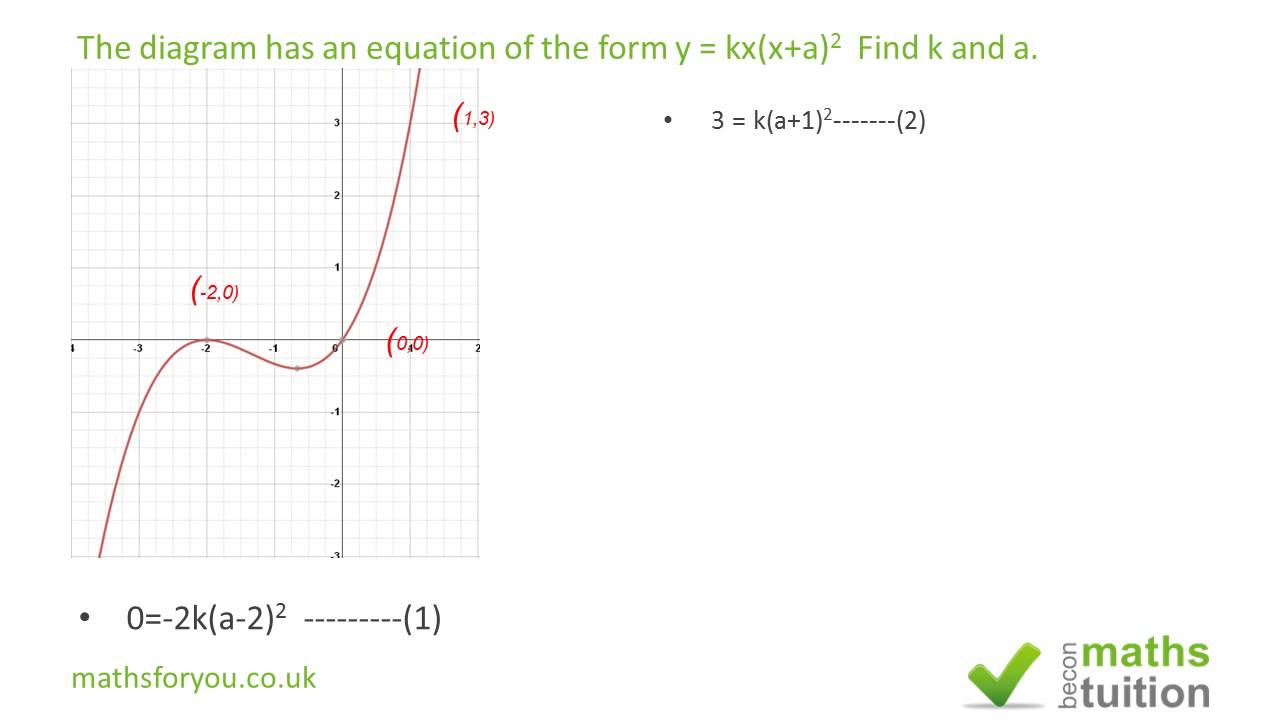
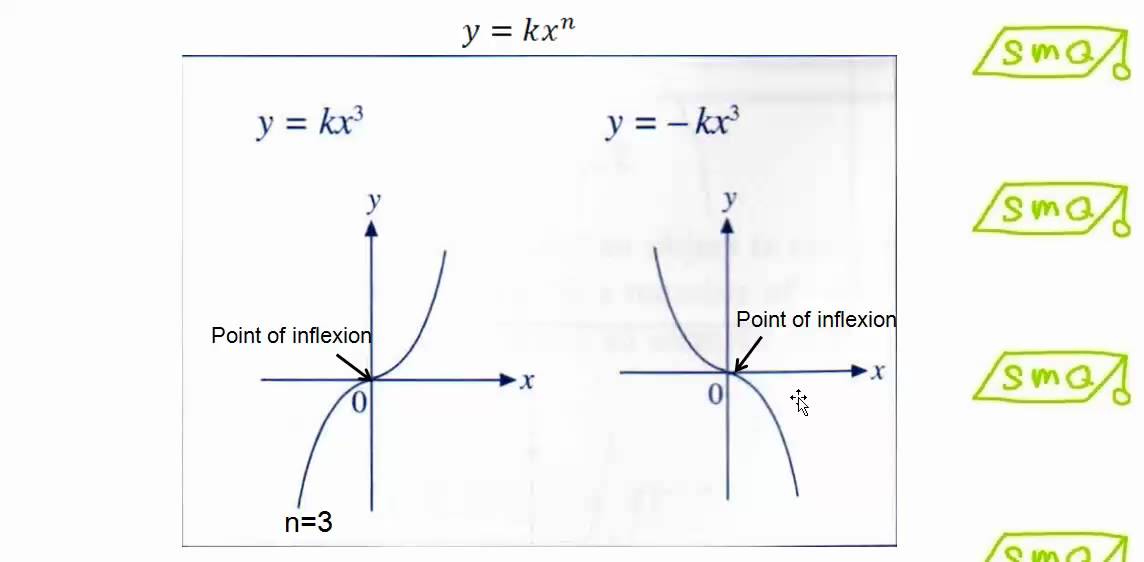
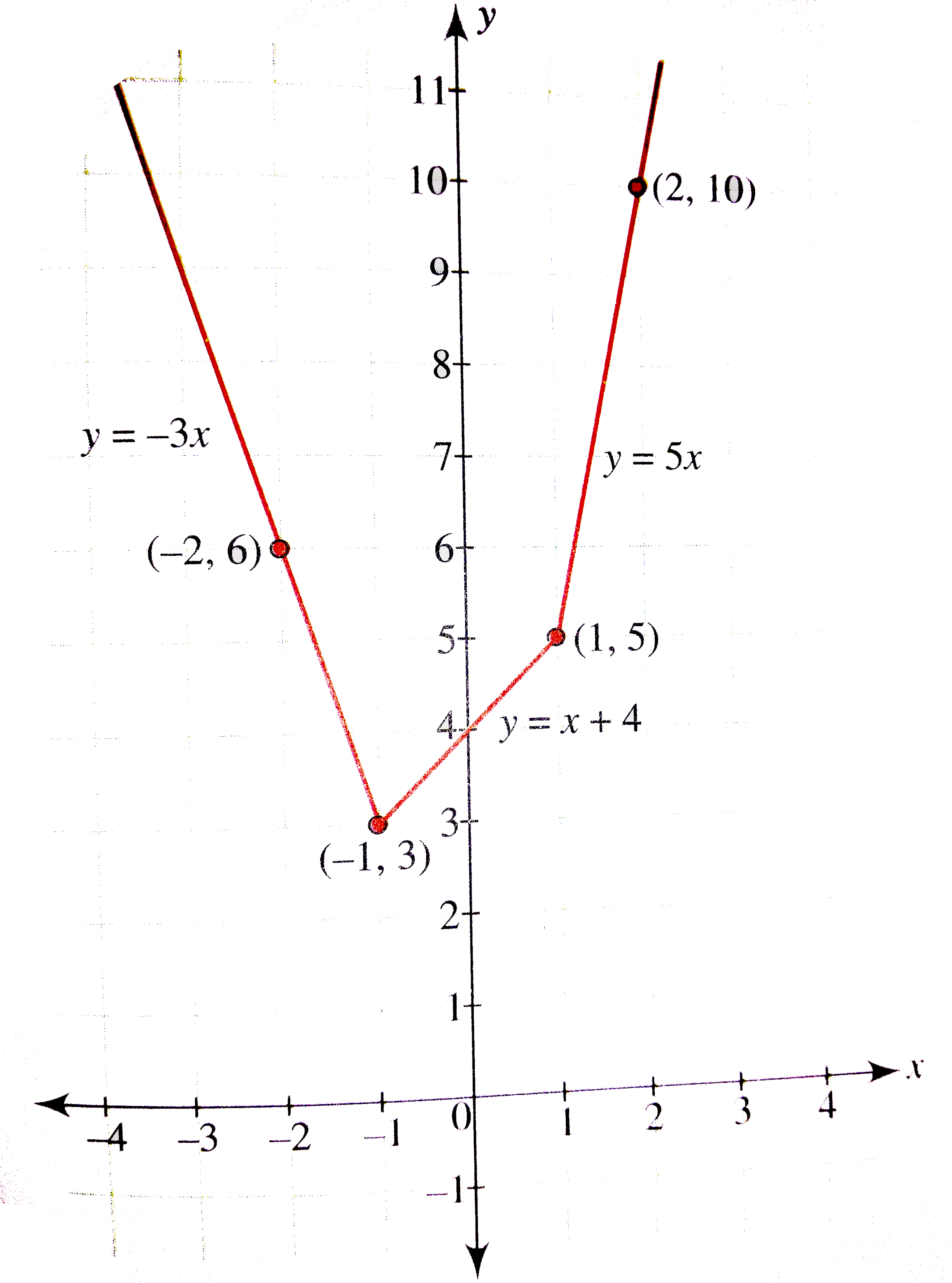
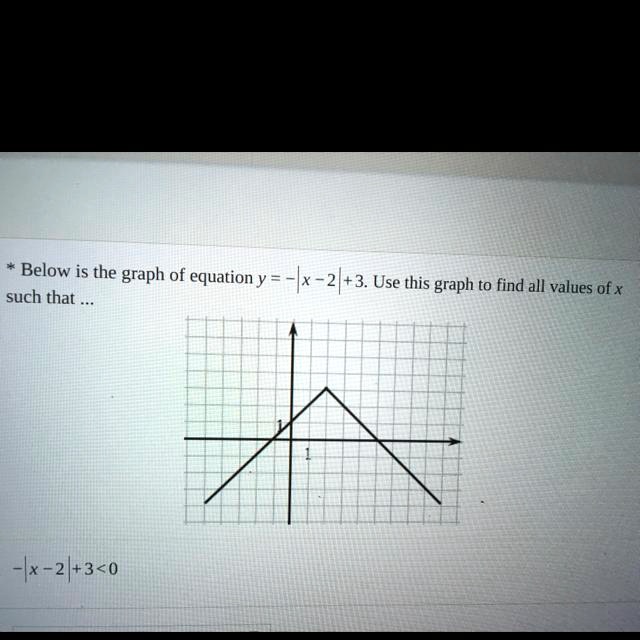
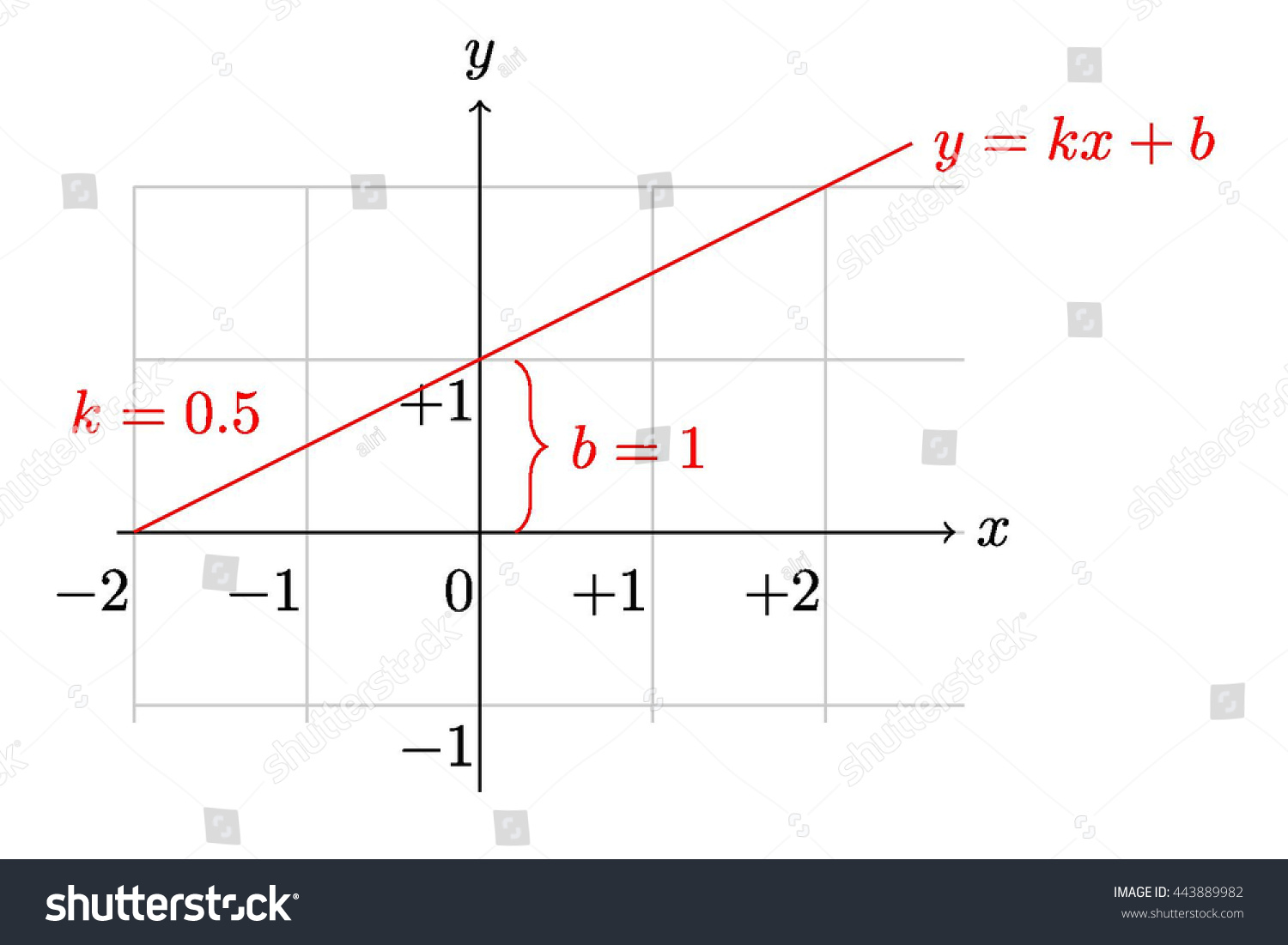
C 1 unit left Which pair of equations generates graphs with the same vertex?Y =kx y = k x Where x and y are variables and k is a constant (a numerical value) x is the exponent and k is the base The yintercept of an exponential curve (at x = 0 ) is 1 since anything raised to the power 0 is 1 The x axis is an asymptote to the curve
Incoming Term: y=k/x^2 graph, inverse square y=k/x^2 graph, y=a(x-h)^2+k graph, (x-h)^2+(y-k)^2=r^2 graph, y=kx^2 graph,
0 件のコメント:
コメントを投稿